Introduction to Differential Geometry for Roboticists:

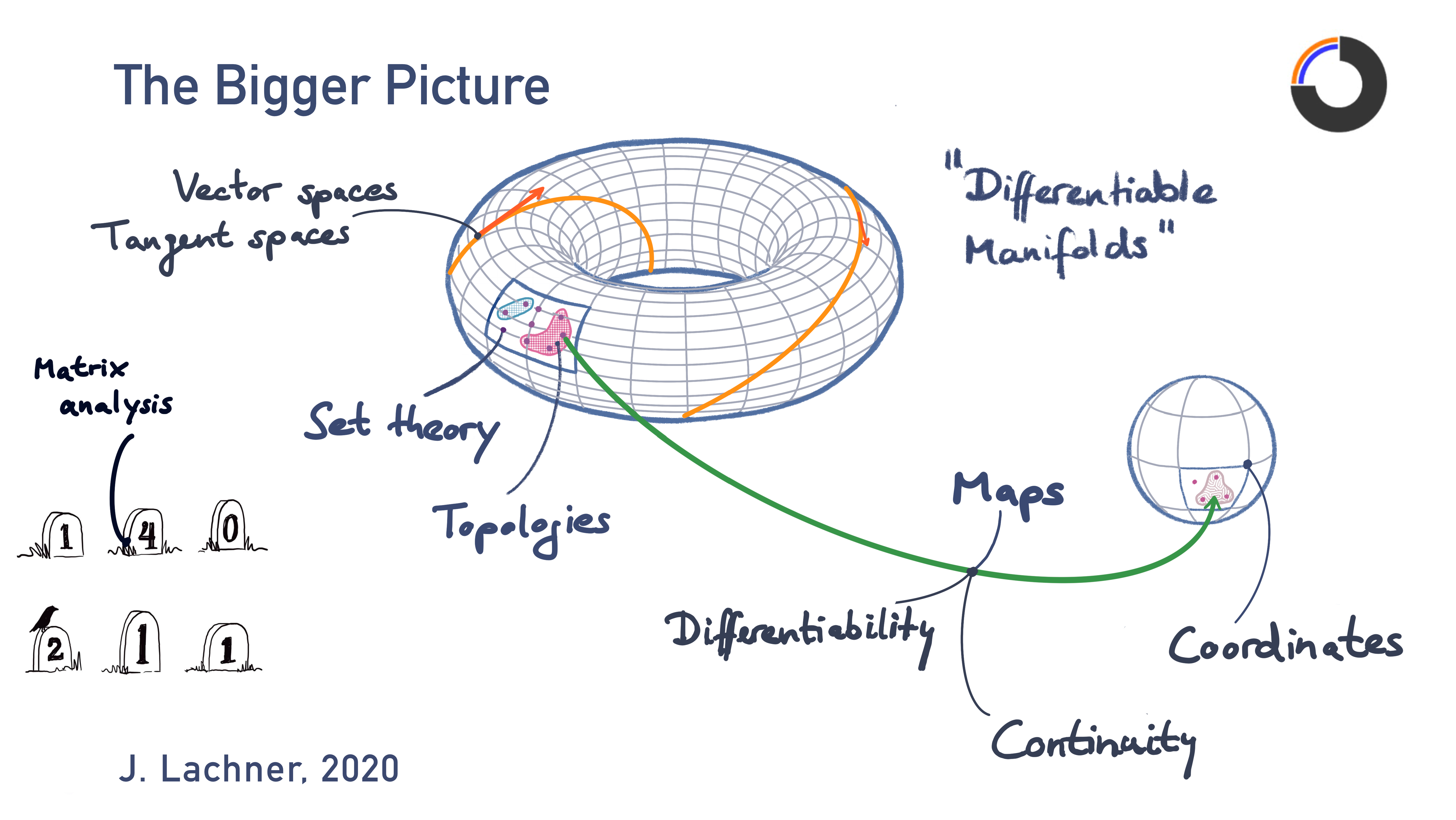
This nine-part tutorial series, titled “Introduction to Differential Geometry for Roboticists,” was designed for MIT MechE undergraduate and graduate students and covers the geometric foundations for describing robot kinematics and dynamics as elements of differentiable manifolds.

Tutorial content

• Set theory and mapping of sets.
• Compositions of maps.
• Topological spaces to discuss convergence and continuity.
• Topological manifolds.
• Viewing manifolds from atlases: chart representations.
• Differentiability of maps, curves, and functions.
• Derivatives.
• Smooth manifolds, curves, and functions; smooth maps between manifolds.
• Vector spaces and dual vector spaces; basis and dual basis; basis change.
• Tangent spaces and cotangent spaces.
• Tensors, tensor spaces.
• Inner product and signature; robotic examples.
• The gradient.
• The push-forward and the pull-back map.
• Lie groups (General Linear Group, Orthogonal Group, SO(n), SE(3)) and Lie algebras.
• Exponential maps; robotic examples to calculate kinematics and dynamics.

Acknowledgements

Thanks to all participants for the nice discussion! Thanks to my former PhD-supervisor Prof. Stefano Stramigioli for teaching me so much about the beauty of geometry.

---