MIT-Novo Nordisk Artificial Intelligence Postdoctoral Fellows Program:

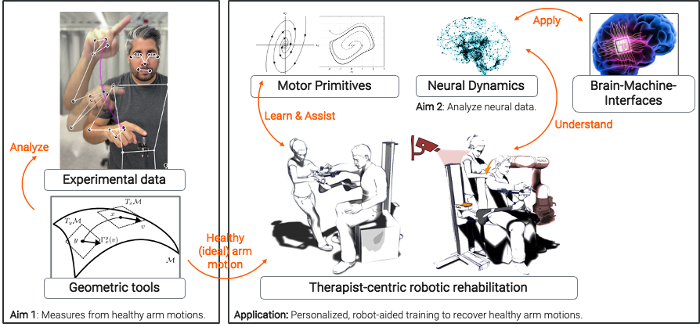
In this project, I aim to quantify human arm movements using Differential Geometry and extend these techniques to neural data to explore how neural populations relate to motor control. By adapting current methods and applying advanced techniques to account for the non-linear trajectories in neural dynamics, I aim to provide insights into neuromotor processes. Artificial RNNs will be trained to model monkey behavior, offering a deeper understanding of these processes. The tools developed in this work can help identify biomarkers aiding in the diagnosis and treatment of neurological injuries.

Aim 1: Extract Quantifiable Measures from Healthy Spatial Arm Motions

Neuromotor control studies traditionally use basic mathematical tools to quantify movement, like orthogonal coordinates for analyzing sub-movements during stroke recovery. These methods work for planar (2D) motions but fall short for curved spatial motions. To accurately quantify these, advanced mathematical tools are needed, treating them as elements of non-linear spaces. I hypothesize that healthy spatial arm motions follow optimized trajectories based on consistent metrics like size, weight, and physical condition. Experiments with healthy subjects and machine-learning-based pose tracking will provide data for analysis using Differential Geometric concepts to identify ideal arm paths. Comparing these paths with those of stroke survivors will help establish a measure of recovery, guiding robot-assisted therapy and tracking patient progress.

Aim 2: Leverage Geometric Invariance to Analyze Neural Data

My second main aim is to apply Differential Geometry to understand human arm motions at the neural level. Motor control results from synchronized neuronal populations, predicting movement direction. However, there is debate over whether these movements use external or body-centered coordinates. This proposal emphasizes coordinate invariance, fundamental in Differential Geometry, for a universal understanding of motor representation. Neural data, spanning hundreds of dimensions, often use PCA for dimensionality reduction, which assumes Euclidean spaces. In this program, I aim to generalize these methods to metric manifold settings, better reflecting neural dynamics. Neurons form complex networks, inspiring artificial Recurrent Neural Networks (RNNs) to emulate neural behavior. Recent successes in low-dimensional RNNs for behavioral data in monkeys highlight the need for revised approaches respecting the neural manifold’s geometry.

Aim 2.1 is to validate differential geometric models with RNNs. I will first learn to process and decode neural data using Prof. Jazayeri’s methods. Then, I will train RNNs to model monkey behavior, evaluating the impact of coordinate choices and geometric metrics on neural dynamics.

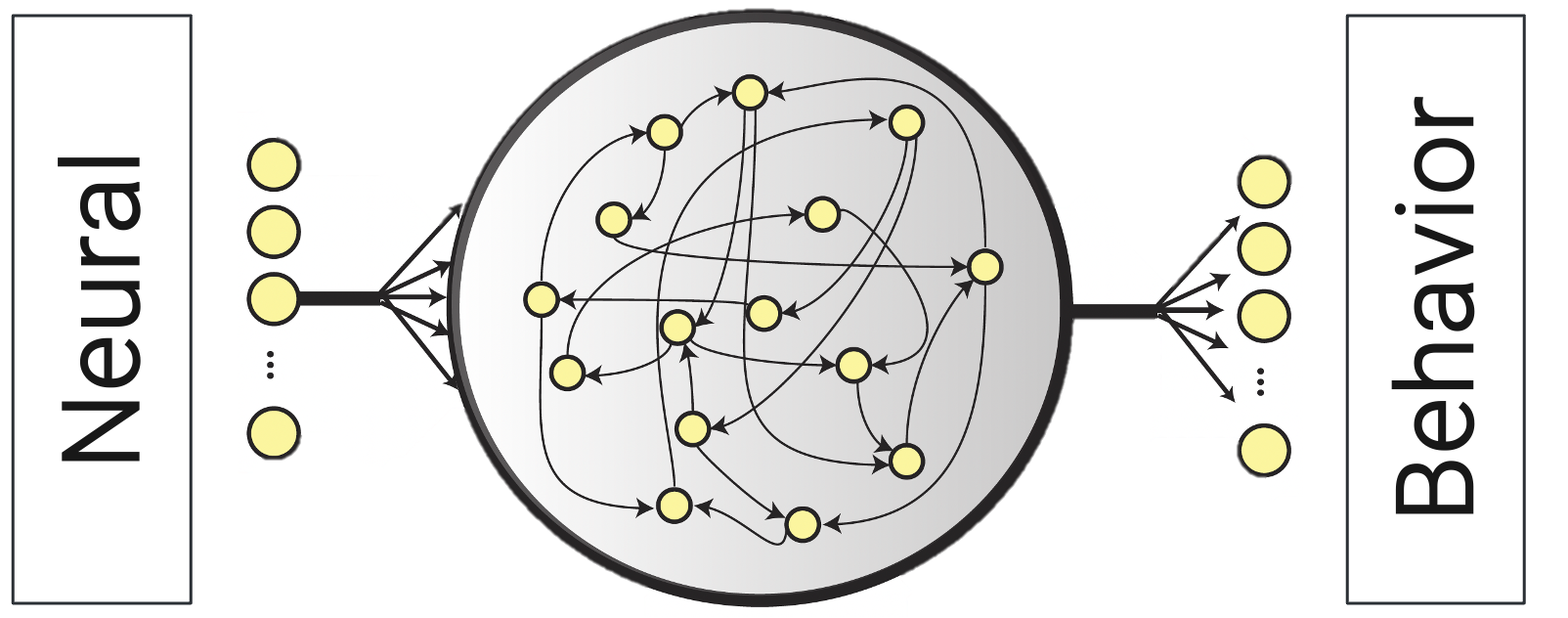
Aim 2.2 is to apply these models to real neural data, analyzing monkey movements during natural tasks. This approach could enhance neural data analysis, providing new insights into movement coordination and advancing biomedical research and neural engineering.

Impact and Research Vision

Understanding the brain’s role in human motor control has considerable practical implications. Neurological disorders originating in the brain often lead to significant motor impairments. Thus, findings at the neural and biomechanical levels in human and non-human primates can contribute to the identification of biomarkers aiding in the diagnosis and treatment of neurological injuries. Furthermore, this work could inform the development of rehabilitation engineering solutions, such as brain-machine interfaces and robotic-based therapy.